蒙特卡羅、動力學蒙特卡羅、分子動力學三者的異同解析

說得更直白一點，傳統的MD和MC基本上是在干同一件事：算積分。只不過最早的MD是在微正則系綜（NVE系綜）里算積分，而最早的MC是在正則系綜（NVT系綜）里算積分。

先說MC

眾所周知，正則系綜里相空間的概率分布就是玻爾茲曼分布

其中H是體系的哈密頓量，?是配分函數，?. 以一維線性諧振子為例，這個相空間概率分布就是下圖所示，其實就是個高斯分布。

知道了概率分布，那么正則系綜中任意平衡態熱力學量M的系綜平均<M>?就是下面這個積分

對于上式中的積分，絕大多數情況下是沒有解析解的，因此只能通過數值求解。最簡單粗暴的用蒙特卡洛方法求解上式積分的方法就是在整個積分區域上均勻地隨機打點，求得每一點處的M(p,q)e^-?H(p,q)值，然后對所有點求和再除以配分函數即可。例如對于一維線性諧振子，我們可以如下在相空間上均勻地打點

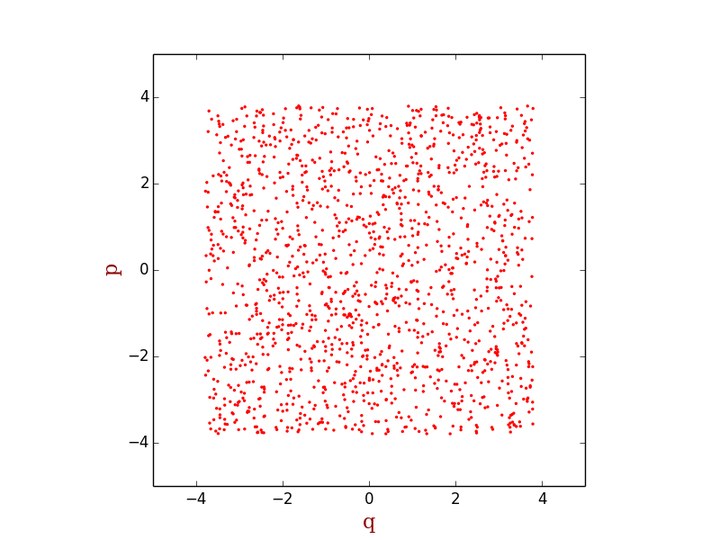
這種算法，的確非常簡單，但效率很低。因為位于相空間中e^-?Η的值非常小的區域，系統處于這個區域的概率非常低，也就是說這些區域大體上來說對系綜平均<M>?的貢獻是非常小的，然而在采樣過程中，由于我們是隨機均勻打點，這樣e^-?Η的值非常小的點和e^-?Η的值非常大的點的權重是一樣的。換句話說，我們浪費了不少時間在那些權重很小的點上。那么是否有這樣算法，能夠使產生的點的分布符合玻爾茲曼分布，也就是說，在e^-?Η的值非常小的區域少打點，在e^-?Η的值非常大的區域多打點（如下圖所示），然后把每一點處的M值相加，就能得到我們需要的系綜平均呢？Metropolis算法就是為了實現這樣的目標產生的。關于Metropolis算法的細節，我不在這里展開，很多書籍里都有描述。

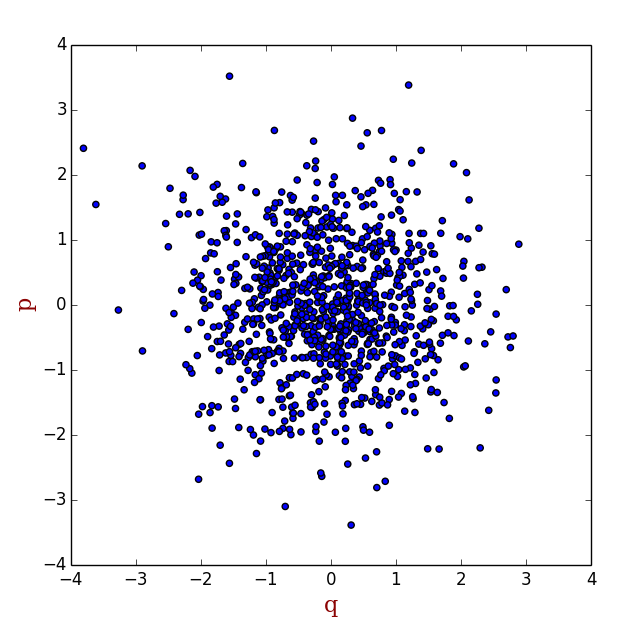
再說MD

MD是基于牛頓方程的，而從牛頓方程是可以很自然導出孤立體系在保守力作用下是能量守恒的，因此最初的MD是在微正則系綜(NVE)里計算系綜平均。根據統計力學的等概率假設，對于總能量為E的微正則系綜，其相空間概率密度分布為P(p,q)=1/Ω(E)，其中Ω(E)是體系處于能量為E時的態密度(density of state)
?那么熱力學量M在微正則系綜里的系綜平均<M>?就是
?其中V是積分的區域，也就是當能量為E時系統所占據的相空間。拿一維線性諧振子作為例子，當能量為E時其在相空間中區域對應于下圖中的圓環，那么這個系綜平均就是根據上式在對應于能量為E的圓環區域上進行積分。MD所做的，就是讓粒子跑遍這個圓環上的每一個點（歷經各態，ergodicity)，把每一點上M的值加起來求平均，得到的就是系綜平均(time average equals ensemble average, this is what we call ergodicity)。

綜上，MD和MC都可看作是為計算系綜平均的采樣方法。采用Metropolis算法的MC不局限于在正則系綜里的采樣，可以應用于其他系綜，比如NPT和巨正則系綜。至于微正則系綜，理論上也可以使用Metropolis算法，只是由于各個態之間能量相等，概率也相等，這時使用Metropolis算法不能起到加速采樣的作用，等于白用。同樣地，MD的采樣也不局限于微正則系綜，當把一個孤立體系和一個恒溫器(thermostat)或者恒壓器(barostat)耦合起來，就可以進行正則系綜或者NPT系綜里的模擬。當然，如果耦合的恒溫器或者恒壓器是以extended Lagrangian形式實現的話（比如Nose-Hoover Thermostat)，廣義上來講MD模擬還是可看作在一個大的微正則系綜中進行。

MD和MC的比較

1、算法的難易程度。一般說來，MD的算法比MC要復雜一些。這是因為，對于MC而言，每產生一幀新的構型只要計算能量然后根據acceptance ratio移動粒子就足夠了。但對于MD，每產生一幀新的構型所需要的不只是能量，還需要每個粒子的速度和受力來對牛頓運動方程進行數值積分，這就加大了計算量。如果還要考慮為了提高計算效率的Verlet neighbor list等設置，MD的算法會更復雜一些。

?

2、所能計算性質的多少。很明顯，MD能比MC計算更多的性質，MC只能計算一些與動力學無關的平衡態性質，比如能量、比熱容等等，MD既可以計算與動力學無關的性質，也可以計算與動力學相關的性質，比如擴散系數、熱導率、黏度、態與態之間的躍遷速率，光譜等等。這是因為，使用Metropolis算法的MC，為了快速得到平衡態的分布，把整個系統簡化為一條馬爾可夫鏈，第N個構型只和第N－1個構型有關聯，與第N－2或者更早的構型沒有什么關聯。在實際情況中不是這樣的，系統是有記憶的，在t₀時刻處于相空間中(p₀,q₀)點的系統與在t₁時刻處于(p₁,q₁)的系統是有關聯的，它們之間的關聯可以用條件概率P(p₁,q₁;t₁|p₀,q₀;t₀)_?來描述。很多動力學性質都和這樣的條件概率有關系，而MD產生的數據是可以計算這些概率分布的。所以世界上沒有免費的午餐，MC雖然算法簡單，但大體上只能計算靜態性質，如果要計算動力學性質還是要上MD。

?

3、可使用的軟件。可使用的MD的軟件遠多于MC的軟件。我個人覺得很大程度上是由于MD能夠計算的性質遠比MC多，并且數據可視化后給人更多直觀的感受。比如說，你可以把MD模擬蛋白質折疊的軌跡文件用軟件可視化之后做成動畫，動畫就比較直觀地演示了蛋白質結構隨時間的變化。可是如果你用MC做同樣一個體系的模擬，你把軌跡可視化之后看到的可能就是一堆原子像無頭蒼蠅一樣亂動，最后穩定在某個構型附近。一般來講，MD軟件的開發也不難，一旦把積分牛頓方程的engine寫好，往里面添加新的相互作用勢并不難，這樣每添加一點新的功能，MD軟件就可以適用于更多的體系。相比起MD軟件的百花齊放，分子模擬中學術界通用的MC軟件并不多，很多課題組都是自己寫MC代碼，但適用范圍僅限于自己研究的體系。

?

4、增強抽樣(enhanced sampling)。這是分子模擬中的一個大坑，不管MD還是MC都會面臨在系綜中采樣不足的問題。

KMC?

Kinetic Monte Carlo(KMC)和主要模擬平衡態性質的MD和Metropolis MC相差就比較遠了，它主要模擬系統隨時間的演化而非平衡態性質。KMC的基本思想是把整個系統劃分成若干個態(state)，并獲得態與態之間單位時間的躍遷幾率（這個可以通過分子模擬或者過渡態理論來計算），然后通過具體的算法決定每一步往哪一個態躍遷，就可以模擬系統在各個態之間隨時間演化。我沒有做過KMC的研究，并不太了解KMC的算法，僅僅粗略看過一兩篇用KMC模擬擴散的文章。以下的例子是我粗淺的理解，可能不太準確。

我們想用KMC模擬粒子在二維晶格上的擴散，并求出擴散系數。假定在單位時間步長內，粒子只能跳到它最相鄰的格點。如圖所示，粒子某時刻處于A格點，那么粒子下一時刻只有可能跳到B,C,D,E格點，單位時間內粒子從A跳到這些格點的躍遷幾率分別為rAB,rAC,rAD,rAE。結合這些躍遷幾率，KMC的算法就可以通過生成隨機數來決定粒子下一步所在的格點。在模擬足夠長時間后我們可以算出粒子的均方位移(mean square displacement, MSD)， 均方位移和擴散系數成正比關系，因而可以求出擴散系數。

當粒子只能在一維情況下運動（即只能從A到B或者從A到D)，并且rAB=rAD， 這種情況下KMC其實就是在模擬一維隨機游走(random walk)。

本文經授權轉載自知乎劉書樂老師的回答：Metropolis蒙特卡羅方法、動力學蒙特卡羅方法、分子動力學方法這三種模擬方法有何特點與差異？

材料牛編輯整理。

材料人重磅推出材料計算解決方案，可提供包括第一性原理、分子動力學、流體力學等方面的計算模擬服務。如有需求，歡迎聯系微信號：iceshigu，或點擊鏈接提交需求，微信端可掃以下二維碼提交。